Obliczanie proporcji to istotna część matematyki, którą można opanować poprzez proste techniki, jak krzyżowe mnożenie czy izolacja zmiennej. W tym artykule przyjrzymy się podstawowym metodom pracy z proporcjami oraz typowym błędom, które warto omijać, aby wyniki były prawidłowe. Dzięki praktycznym przykładom i wskazówkom dowiesz się, jak efektywnie posługiwać się proporcjami.
Spis treści
Podstawowe metody obliczania proporcji
Proporcje stanowią kluczowe narzędzie w matematyce do porównywania różnych wartości[1]. Istnieje kilka prostych metod, które umożliwiają efektywne ich obliczanie.
- mnożenie krzyżowe pozwala na szybkie rozwiązywanie równań proporcjonalnych,
- izolacja zmiennej upraszcza obliczenia poprzez wyodrębnienie jej z równania proporcji,
- użycie narzędzi takich jak Excel czy kalkulatory zwiększa precyzję i przystępność pracy z proporcjami.
Mnożenie krzyżowe polega na mnożeniu wartości przeciwnych na krzyż, co upraszcza proces i ułatwia dojście do wyniku[1]. Kolejną metodą jest izolacja zmiennej, która pozwala na wyodrębnienie jej z równania proporcji, co znacznie upraszcza obliczenia. Przykładowo, w równaniu 3:x = 6:9, możemy skupić się na x. Prowadzi to do równania 3*9 = 6*x, co ostatecznie daje x = 4,5.
Proporcje mają wiele praktycznych zastosowań w codziennym życiu.
- w kuchni, gdzie odpowiednie proporcje składników decydują o smaku potraw,
- w finansach, gdzie są pomocne przy analizie danych, jak obliczanie VAT od ceny produktu.
Umiejętność pracy z proporcjami jest zatem nieoceniona zarówno w teorii matematycznej, jak i w praktycznych sytuacjach. Aby ułatwić obliczanie proporcji, można sięgnąć po narzędzia takie jak Excel czy kalkulatory, które szybko i precyzyjnie wykonują potrzebne operacje. Dzięki tym narzędziom, praca z proporcjami staje się mniej skomplikowana i bardziej przystępna, co zwiększa naszą pewność siebie w codziennych wyzwaniach matematycznych.
Jak działa metoda krzyżowego mnożenia?
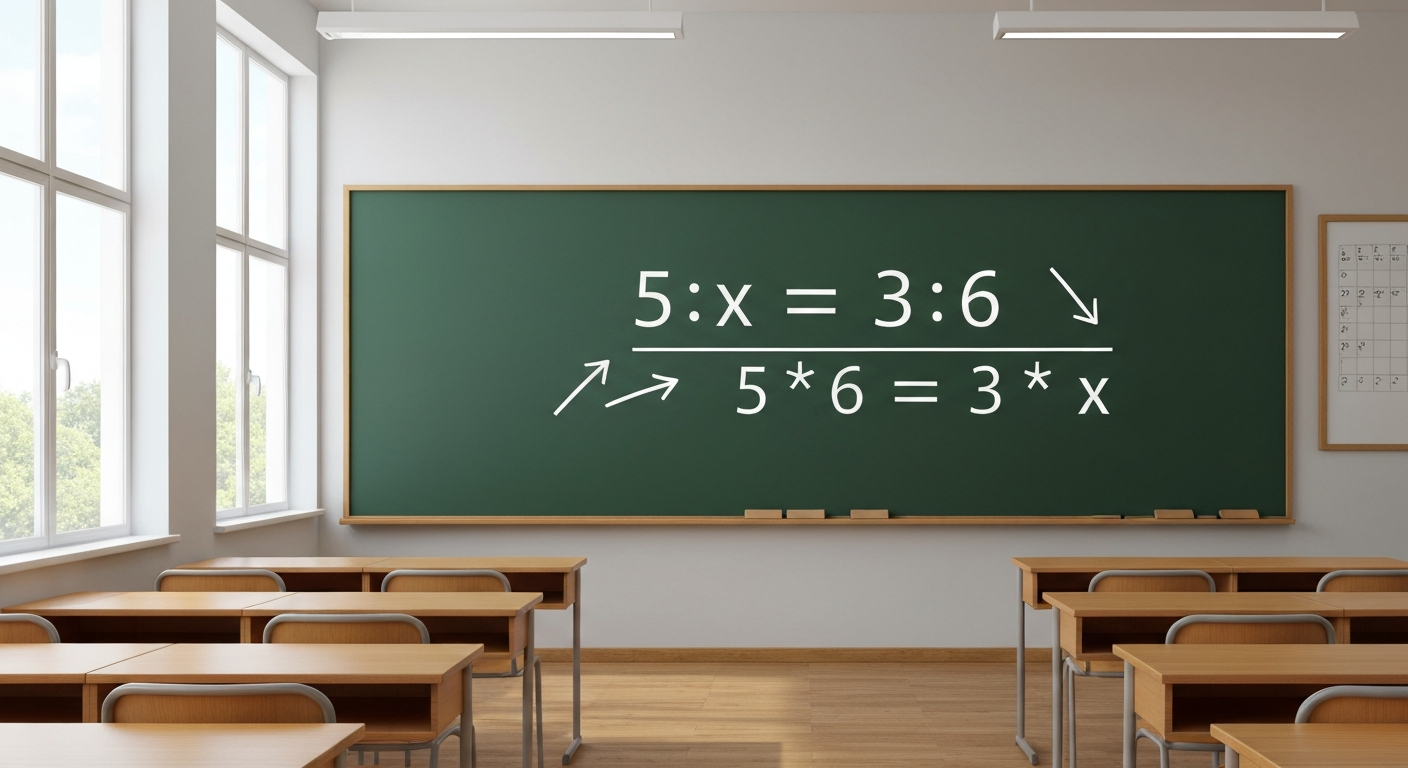
Metoda krzyżowego mnożenia znacząco ułatwia rozwiązywanie proporcji poprzez tworzenie prostego równania. Wystarczy pomnożyć wartości po przekątnej. Na przykład, dla proporcji a/b = c/d, krzyżowe mnożenie daje równanie a * d = b * c. Następnie wystarczy rozwiązać to równanie, aby znaleźć niewiadomą.
Przyjrzyjmy się temu na przykładzie: mamy proporcję 5:x = 3:6. Krzyżowe mnożenie prowadzi do równania 5 * 6 = 3 * x.
Po podzieleniu obu stron przez 3, uzyskujemy x = 10. Ta metoda jest intuicyjna i pozwala szybko rozwiązywać proporcje.
Rozwiązywanie równań poprzez izolację zmiennej
Izolacja zmiennej to technika ułatwiająca rozwiązywanie równań poprzez wyodrębnienie szukanej wartości[1]. Wymaga przekształcenia równania w taki sposób, aby zmienna znalazła się po jednej stronie. Przykładowo, w proporcji 3:x = 6:9, po wykonaniu krzyżowego mnożenia otrzymujemy 3 * 9 = 6 * x. Następnie dzielimy obie strony przez 6 i uzyskujemy x = 4,5. Dzięki temu proces obliczania proporcji staje się bardziej efektywny i prostszy. Takie podejście jest niezwykle przydatne w rozwiązywaniu problemów algebraicznych, ponieważ pozwala szybko i precyzyjnie odnaleźć wartość zmiennej.
Typowe błędy i jak ich unikać
W trakcie obliczania proporcji często natrafiamy na błędy, które mogą prowadzić do niewłaściwych rezultatów[1]. Kluczowe jest zrozumienie zasad proporcji, aby unikać typowych pomyłek[1]. Często zdarza się pomylenie wartości skrajnych ze środkowymi. Aby temu zapobiec, warto jasno określić, które liczby są skrajne, a które środkowe.
Kolejnym problemem jest nieprawidłowe przekształcanie jednostek. Zawsze należy upewnić się, że stosowane jednostki miary są zgodne[1]. Ponadto, pomijanie etapów w obliczeniach to częsty błąd. Aby go uniknąć, warto zapisywać poszczególne kroki i dwukrotnie weryfikować wyniki.
Podwójna kontrola wyników pozwala upewnić się, że są one sensowne i zgodne z danymi wejściowymi. Dzięki takim strategiom można zminimalizować ryzyko pomyłek podczas obliczania proporcji, zapewniając tym samym precyzyjne rezultaty[1].
Częste błędy podczas obliczania proporcji
Podczas obliczania proporcji często występują błędy, które mogą prowadzić do nieprawidłowych rezultatów. Jednym z bardziej powszechnych jest pomylenie wartości skrajnych z centralnymi w równaniach proporcjonalnych. Aby tego uniknąć, należy wyraźnie wskazać, które liczby są skrajne, a które środkowe.
Innym problemem bywa niewłaściwe przekształcanie jednostek. Kluczowe jest, aby przed rozpoczęciem obliczeń wszystkie jednostki były zgodne. Dodatkowo, częstym błędem jest pomijanie kroków podczas obliczeń. Zapisując każdy etap i dokładnie sprawdzając wyniki, można zminimalizować możliwość pomyłek. Dzięki tym praktykom obliczanie proporcji staje się dokładniejsze i bardziej wydajne.
Jak poprawnie interpretować wyniki proporcji?
Prawidłowe zrozumienie wyników proporcji odgrywa kluczową rolę w uchwyceniu relacji między różnymi wartościami. Proporcje stanowią istotne narzędzie w analizie danych, ukazując, jak jedna wartość odnosi się do innej. Przykładowo, proporcja 2:1 wskazuje, że pierwsza liczba jest dwukrotnie większa od drugiej. W kontekście statystyki, interpretacja proporcji może ujawniać powiązania między zmiennymi, co ma znaczenie zarówno w badaniach naukowych, jak i analizach rynkowych. Zrozumienie tych relacji umożliwia podejmowanie lepszych decyzji opartych na danych.
Źródła:
- [1] https://trygonometria.edu.pl/obliczanie-proporcji-w-matematyce-proste-metody-i-praktyczne-przyklady
- [2] https://www.ortofrajda.pl/obliczanie-proporcji-dla-nauczycieli-matematyki-przewodnik-krok-po-kroku/
- [3] https://zssio.com.pl/obliczanie-proporcji-w-matematyce-proste-metody-i-praktyczne-przyklady-ktore-zrozumiesz
- [4] https://doklasy.pl/obliczanie-proporcji-w-matematyce-jak-obliczyc-proste-metody-i-praktyczne-przyklady/
- [5] https://szaloneliczby.pl/proporcje/
- [6] https://www.youtube.com/watch?v=BpxhX_4x7rU
- [7] https://zpe.gov.pl/a/rownania-w-postaci-proporcji/DHi3H5hIa
- [8] https://opracowania.pl/opracowania/matematyka/proporcja-i-jej-wlasnosci,oid,1818
- [9] https://magu.pl/proporcja-kalkulator
- [10] https://www.youtube.com/watch?v=n9TREql81-A

Doktor nauk humanistycznych, z mediami związany od 15 lat. Odpowiedzialny za linię programową portalu Scholaris.pl. Czuwa nad merytoryczną poprawnością artykułów i kieruje pracą całego zespołu. Pasjonat historii nowożytnej i nowych technologii w edukacji.